Cell Automata JAVA Program

Instructions for using the CellAutomata JAVA program.

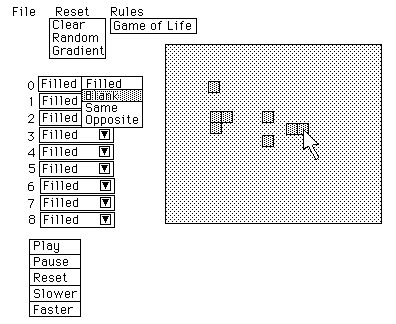
This is a diagram of the screen pattern that appears when you run the CellAutomata program.

By using the mouse to "click" in the field on the right, above, you can cause any of the small squares to become "filled". The Pull-Down menus along the middle of the left side allow you to chose the "rules" that will be obeyed in repeatedly recalculating which squares should become filled, which squares should become blank, which squares should remain the "same". ("same" means to remain filled if filled, to remain blank if blank) or to change to the opposite (i.e. to become blank if currently filled, and to become filled if currently blank). For example, the famous "Game of Life" results from the following combination of rules: Squares that currently have 3 filled neighbors become filled; Squares that currently have 2 filled neighbors remain the same; Squares that currently have 0, 1, 4, 5, 6, 7 or 8 filled neighbors become blank. One of the pull-down menus along the top sets the rules to be the "Game of Life" But this is just one of 262,144 alternative combinations of rules. (4 to the ninth power) So if you spend one second on each set of rules, it will take you a little more than three days to try them all. Therefore when you find some interesting effect, it is wise to make a note of the set of rules that produced it, because it may not be so easy to find again. One interesting set of rules is for squares to become blank when they have 0, 1, 2, or 3 filled neighbors, to remain the same when they have 4 filled neighbors, and to become filled when they have 5, 6, 7 or 8 filled neighbors. Try setting the field to a random pattern, using the "Reset" pull-down menu along the top row, and then watch the effect of this set of rules. What category of phenomena does it resemble? Why? Could you have deduced the general nature of the result beforehand? (Honestly?) In this cellular automaton, the squares are light blue the first time they become filled, become dark blue when filled for two generations in a row, and become black when filled for three or more generations in a row. Otherwise, however, all squares only have two values, 0 (blank) and 1 (filled). It is not difficult to write programs like this one in which each square can have more than two alternative values; for example, we might let each square have any of the values 0, 1 or 2. Then the rules could be based on adding up the numbers of all the immediate neighboring squares, which would mean that the sum of the neighbors could be any number between 0 up to a maximum of 16. Then the total alternative combinations of rules would be 4 to the seventeeth power, which happens to be seventeen billion, a hundred and seventy-nine million, etc. Actually, you would also have more choices for each of the seventeen alternative possible sums of neighbors. For example, squares that now have the value 1 and the sum of whose neighbors is (say) 5 could be reassigned the value 0, 1 or 2. Alternatively, you could count only the neighbors directly above and below, and directly to the right and left (i.e. not count diagonal neighbors) in which case the maximum sum is 16 when squares can have 0, 1, or 2 as their values. Even so, there are still more alternative choices, because you might reassign squares that now have 0 to become either 1 or 2, etc. I would like to put a really general program on line that lets the user chose how many alternative values each square should have (2, 3, 10, etc.), to decide which other squares should be counted as neighbors, and to specifiy what action should be taken for each of the (really large!) numbers of alternative sums or averages, or differences, or whatever currently exists among each square's neighbors. Please do not think that such arbitrary rules have no comprehensible relations to to the prediction of reality. Consider a cellular automaton in which each square is allowed to have any of the values 0, 1, 2, 3, 4, 5, 6, 7, 8 or 9. Then let the rules be that the values of each squares' neighbors is added up, averaged, this average compared with the current value of that square itself, and that square decreasing in value when its current value is larger than the average of its neighbors, and increasing when its current value is smaller than the average value of its neighbors. This simulates diffusion very economically. 33333333333333333333333333330 85444443333333333333333332210 86554444444433333333333322210 87655544444444443333333322110 87665555444444444433333222110 87766655555444444444333222110 87766655555544444444333322110 87776666555555444444433322110 88776666555555554444443322110 88776666655555555544444332210 88766666665555555555444433210 87776666666655555555554443210 87776666666666666655555544320 87666666666666666666555555430 66666666666666666666666666660 In order to simulate the physical distortions of elastic materials, then each square needs to contain three independent numbers (representing positions along the X, Y and Z axes, and for the " recalculation rule" to calculate differences in these values from those of the immediate neighbor squares, to take the square root of the sums of the squares of these distances, to apply a proportionality equation which plays the role of an elastic modulus, etc. etc. Any computer program that simulates spatial variations by diffusion, attraction, repulsion, or any other interaction, will have at the core of this simulation something equivalent to a cellular automaton. For my class in Embryology, I ask the students to use the JAVA cellular automata program to explore the consequences of the following. #1) Change the settings for 0, 5 and 6 neighbors to "Blank", then click on a corner square in the playing field area to the right; and then click on "Play". #2) Describe what happens. #3) Do the patterns generated have any plane of mirror image symmetry? #4) Do all the patterns have this symmetry, or just some of them? #5) Go to the upper row of pull down menus, and click on "Game of Life" (while the previous patterns are still running) #6) Are the flashing patterns still symmetrical? #7) Let the patterns run for a while until they calm down, and you get mostly just regular patterns of black squares. Why have these stopped moving? #8) Do these individual small black stable patterns have any individual symmetries? Make a list, which can be a series of small drawings. #9) Next change the setting for "4" neighbors so that it reads "same", instead of "blank". Does anything happen? Why or why not, in your opinion? #10) Then click on any of the squares next to one of the stable patterns: what happens? (give it time to develop) Does this look anything like the growth of an organism? #11) Reset all numbers, 0 through 8 to filled; wait a bit, and then set 0 and 8 to "blank". Try not to get hypnotized. #12) Explore the consequences of different sets of "rules", like "Blank" for 0, 1, 2, 3. "Same" for 4, and "Filled" for 5, 6, 7 and 8. And then click on "Random" in the pull-down menu along the top labeled "Reset"

 

to the program

back to Harris home page