Embryology Biology 441 Spring 2007 Albert Harris
Those questions in ITALICS are more difficult than you need to understand for the exam
1) The surface of what shape has the same (non-zero) curvature in every direction at every point on its surface?
2) A bigger circle has a (larger? smaller? the same? you can't necessarily tell?) curvature than a smaller circle?
3) Consider an ordinary light bulb, that looks like this: 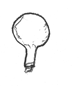
-
a) What parts of its surface have the same curvature in all directions?
b) What parts of its surface have zero curvature in two (exactly opposite) directions?
c) What parts of its surface consist of "saddle points" whose maximum curvature is positive in one direction, but which has a negative curvature in the perpendicular direction (or axis)?
-
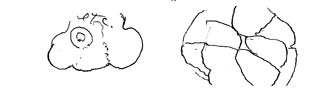
a) The embryos of most species, from early oogenesis until after gastrulation begins?
b) The aggregated mass of Dictyostelium amoebae, before it forms a slug?
c) An early limb bud, before it develops its asymmetries (in its ant.-post. and dorso-ventral axes?
d) Soap bubbles and water drops
e) Dead cells
6) a) If you weaken the tension in part of the surface of a balloon (for example, if you put some chemical on it that reacted with the rubber, and weakened it), then how would that change the size and shape of the balloon? b) What if you somehow made part of the rubber more contractile?
7) If the tensions in the rubber of an inflated balloon (at most locations on the surface) are twice as strong in one direction as they are in the perpendicular direction (that is, in the direction perpendicular to that in which they are stronger) then predict the shape of the balloon.
8) When an artery bursts because of excess blood pressure, can you predict the direction of the long axis of the rip in the artery wall?
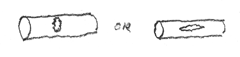
9) The smooth muscles and collagen fibers that form most of the walls of your arteries are oriented with their long axes pointed nearly all in what direction, relative to the long axis of the artery?
10) Imagine that some disease caused these smooth muscles and collagen fibers to become reoriented, equally in all directions parallel to the surface of the artery: would you survive? (hint: aneurism)
11) Would you agree with the explanation that this result was caused by "weakness of the artery wall?"

12) If an organ (or an organism) is shaped by two (or more?) exactly counter-balanced forces (of any kind), then if both forces have spherical symmetry (the same strength in all directions), then what shape will the organ (or organism) be, whose shape is caused by these forces?
13) Is this shape caused by minimization of thermodynamic free energy, as many people claim, and believe that this is a very deep insight? No, that's a mistake! Whether free energy is minimized depends on whether the forces a re reversible and conservative, not whether they are counter-balanced
14) If this organ (or organism) then spontaneously changes to some shape with a different symmetry, then can you deduce from that something about the directional symmetry of whatever forces cause this spontaneous change in shape? (hint: yes; those new forces have to be asymmetrical)
15) The brain and spinal cord start out as a hollow, liquid filled cylinder. Then the brain expands greatly relative to the spinal cord, with some parts (mid-brain, forebrain, eye-cup) bulging outward more than others. Argue whether these differences in swelling are caused by changes and differences in tension in different parts of the wall of the brain, or by changes in fluid pressure, or by "growth". How will brain shape be controlled by weakening of tension in some directions relative to others?
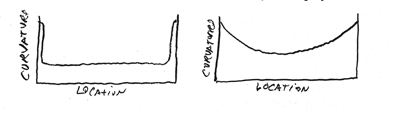
16) Consider the following two graphs of amounts of curvature in two perpendicular directions on the surface of a hollow ball. Figure out what game is played with this ball!
17) Try to visualize a solid shape whose surface has zero curvature in one direction, and whose curvature in the direction perpendicular to this is some constant amount. This solid shape is called a what? Can you draw one? And draw arrows in different directions on its surface, with the length of each arrow being proportional to the amount of curvature in that direction.
18) Next, visualize a different solid shape, in which the curvature of the surface is zero along one axis (that is, in two opposite directions), and in the axis (directions) perpendicular to this, the curvature of the surface varies linearly (in the sense that this curvature might be 10 degrees per millimeter in one area, and 11 degrees per millimeter a certain distance away, and 12 degrees per millimeter twice that distance away. This shape has a familiar name; what is that name? If in doubt, write or sketch your reasoning. Are any biological structures this shape, at least approximately. How do you suppose genes cause such biological structures to form?
19) What is meant by saddle-points, in terms of the curvature of a surface? For the following objects, do any parts of their surfaces consist of saddle points? And please draw those parts (if any) that do consist of saddle points, for a) A cell, late in mitotic division? b) An ordinary light bulb? c) The surface of one of your hands? d) A branch-point in a blood vessel? e) The surface of the brain in early development? f) The surface of a teleost fish egg at the one-cell stage? g) A slime mold slug?
20) At saddle points, are there certain directions in which the local curvature is zero in two directions? From what logical argument do you reach this conclusion?

21) If you dip a ring in a soap solution in water, then a continuous soap film will remain, stretched across the ring: In terms of the forces that cause its shape, then why is this soap film flat? What curvatures does a flat surface have?
22) If you had a circle or ring made out of metal, and bent parts of this metal ring so that they were not all in the same plane, and you dipped this in a soap solution, and took it out, and a continuous sheet of soap formed across the interior of this bent ring, then this soap film will NOT be flat. However, at each point, if you measure the curvatures in any two perpendicular directions, and add these two curvatures together, the sum of these curvatures will be what constant amount?
23) On this non-flat soap film, are any of the points saddle-points, in the sense that curvatures in perpendicular directions are "negative" relative to each other?
24) No matter how complicated or irregularly you bend the edge of such a ring, the soap film inside it will always be shaped so that what (?) rules are obeyed by the curvatures at each point on the film.
25) If you stretch a thin rubber sheet across such an irregularly bent ring, then what rules govern the local curvatures at each point? (as compared with the curvature in the perpendicular direction at that same point? as compared with the curvatures at other points on the same rubber surface?)
26) I have drawn an ellipse. ![]()
Can you draw a graph of the relative amounts of curvature of the ellipse at all the different points around its periphery?
27) I have drawn an eye-ball in side view. 
Can you draw a graph of the relative amounts of curvature at each point around its surface, as seen in this drawing?
-
a) The curvatures along the direction parallel to the sheet of paper?
b) The curvatures at each of the same points in the direction perpendicular to the paper?
29) If you have two soap bubbles, stuck together so that there is only one soap film along the side where they touch, then if one soap bubble has a smaller diameter than the other, the side of the smaller bubble will always bulge into the side of the bigger bubble. Can you explain this in terms of an equation relating P, T and C?
30) In this situation, there are effectively three curved soap films, each of which has a different surface curvature (C1, C2 and C3), and within ech of the three the curvatures are the same in all directions at each point. Can you figure out a simple algebraic equation that relates these three curvatures to each other, and to the pressures inside the two bubbles?
31) Two rubber balloons, sharing a common side, would not obey this same equation, unless the tensions in different parts of their rubber surfaces happened to have what properties?
32) In a case of two such rubber balloons sharing a common side, if one balloon had a smaller diameter, but did NOT bulge with a convex surface toward the larger balloon, then what could you conclude about the pressures in the two balloons, and how much force is required to stretch different parts of their surfaces in different directions?
33) If you had a balloon that is NOT spherical when inflated (maybe shaped like Mickey Mouse's head) could you figure out the different amounts of tension in different parts of its surface based on observing or measuring the curvatures at different places on its surface?
34) In a cylindrical pipe, or hose, or balloon, only the tensions in the circumferential direction contribute to resisting outward pressure. Do you see why that is true? Hint: what does it have to do with the amounts of curvature in the longitudinal compared with the circumferential direction?
35) If you have a balloon that becomes cylindrical when inflated (but of course has hemispherical ends) sort of like a hot dog, then when this balloon is only half-inflated it will have the shape drawn below. What are the curvatures in different parts of a surface with this shape?
Are there differences in air pressure from one part of such a balloon and another part?
When you push in on different parts of this balloon's surface why does it feel like the air pressure is much larger in the more inflated part?
In which parts is the rubber stretch more tightly?
Try to draw a map of the differences in amount and direction of tension of the rubber that the balloon is made out of in different parts of this partially-inflated balloon.
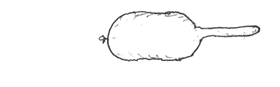
36) How can scientists measure the amounts of tension in different parts of a developing embryo?
37) How can genes create anatomical shapes by changing amounts and directions of mechanical tension in cells, sheets of cells, collagen gels, and other parts of the body?
38) How can computers predict what anatomical shapes will be caused to form, based on tensions?