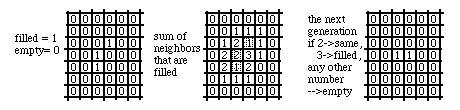
A typical example would be an array of squares, arranged like those of a chessboard, with each square being assigned a value of either one or zero (instead of "one", you can say "filled", and instead of "zero" you can say "empty"). You start out with an initial pattern of some squares filled and other squares empty, and you have a set of rules for calculating the next "generation". One set of rules would be that any square that has two filled neighbors will stay the same in the next generation as it is now; and any square that has 3 filled neighbors will become filled (whether it was filled in the current generation, or not); but any square that has 0 filled neighbors, or 1, or 4, 5, 6, 7 or 8 filled neighbors will become empty, whether or not it is now filled. This set of rules was applied to the pattern on the extreme left below, in order to generate the pattern on the extreme right. Do you see why the pattern will "die out in the next generation is this set of rules is applied one more time?
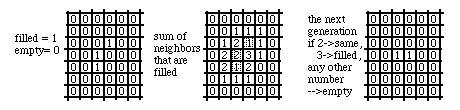
In fact, this particular set of rules (3->filled; 2->same; any other number->empty) are those of what is probably the best-known (and most studied) of all cellular automaton, namely the "Game of Life", invented by the British mathematician John Conway and popularized by Martin Gardner's "Mathematical Games" column in Scientific American magazine in 1970-1. A share-ware program for playing this game is included on the program disk. This game can be surprisingly addictive; in the early 1970s it is estimated that between 2 and 3 billion dollars a year worth of main-frame computer time was used up by programmers exploring this game without their bosses' permissions.
This clandestine programming led to the discovery of such things as gliders, glider guns and many other strange beasts. Conway claims to have chosen these rules to mimic some ecological phenomena; others have subsequently found other combinations of rules which really do simulate certain interactions among animal populations. Other cellular automata are used in computer simulations of chemical reactions, gas flow ("lattice gases"), neutron chain reactions and who knows what else. The topic was jointly invented at Los Alamos by two of the brightest and most infuential men of this century, John Von Neumannand Stanslaw Ulam (the former invented the CPU style of computer architecture; the second held the patent on the hydrogen bomb!).
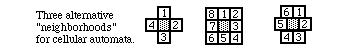
Dozens of books and thousands of research papers have been written about cellular automata. There are many variant forms: you can have hexagonal and triangular neighborhoods as well as square ones, you can decide to count only the 4 orthogonal neighbors (above, below, left, right) and omit the diagonal ones; or you can also count positions some distance away; for example, one of the programs on the disks counts 24 neighbors for each square. In addition, the number of different alternative values that each "cell" can be more than 2 (filled or empty); they can have values of 0, 1, 2, 3 etc. Furthermore, the recalculation rules can be based on something other than simply adding up filled neighbors. Computers are good at this sort of thing: indeed, many things that one tries to simulate almost "try" to turn themselves into cellular automata. For example, if the numerical value of each square tends to approximate the average value of its immediate neighbors, then the result will be a simulation of ordinary diffusion. If the calculation of new generations is based on the ratio of near neighbors to far neighbors (with near ones stimulating and far ones inhibiting), then the system's behavior will generate patterns like those of reaction diffusion systems, such as those of Turing that will be discussed below.
Consider this set of rules: each square can have a value of either 0 or 1 or 2 or 3; any square having a value of 1 will always become a 2 in the next generation; any 2 will become a 3; and any 3 will become a 0; but any 0 that is next to a 1 will itself become a 1 in the next generation. Can you see what the net behavior will be? Can you see why it will "simulate" propagation of nerve impulses? (What corresponds to the refractory period?) It can also simulate forest fires!
Cellular automata can also be one-dimensional (i.e. along a line, usually with sequential generations being represented below each other down the page), two-dimensional (like the game of life) or 3-dimensional (with neighbors above and below the plane of the page).
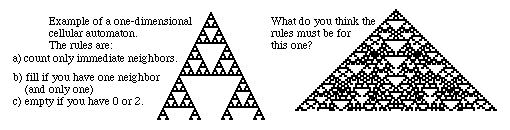
The two examples above were obviously initiated at single "filled" squares. But what if the initial pattern contained some kind of random mixture of filled and empty squares? Here is an example:

Which of the sets of rules does the cellular automaton above seem to be obeying?
In what way is the initial pattern non-random?
The color patterns on several species of cone shells happens to have very much this particular pattern.
What do you conclude from this? What might be the explanation? Are there alternatives?
The major guru of cellular automata these days, especially one-dimensional cellular automata is a British whiz kid named Stephen Wolfram (who is also the author/owner/president of Mathematica, a set of expensive software for doing calculus and other higher math on a computer, which costs >$700!).
If you experiment with different sets of rules, you find hundreds or even thousands of different behaviors, but these fall into a few main patterns including

One of my favorite facts about cellular automata is that if the rules are these:
Fill if you have an odd number of neighbors; Empty if you have an even number (or zero neighbors).
The result is to duplicate the original pattern infinite numbers of times!!
In fact, this is only a special case of a more general theorum which is that if the rules are of this form:
Fill if sum of neighbors modulo any prime number; otherwise become empty.
(the "fill if odd, empty if even" rule above is the special case where the prime number is 2)
Rules of this class will multipley duplicate any initial pattern, for 1, 2 or 3 dimensional automata, and for any definition of what is a neighborhood.
2) B catalyses its own breakdown and also catalyses the breakdown of A.
3) B diffuses faster than A.
We can follow, step by step, how such patterns are generated by considering the result of a small, local increase in the concentration of the A substance. Since A catalyses its own synthesis, a local increase in its concentration will lead to a further increase; so a peak in A concentration will grow spontaneously at the site of the original perturbation. In addition, since A also catalyses the synthesis of B, a peak of B concentration will also form spontaneously at this same location, the two peaks being superimposed on each other. However, because the B substance diffuses faster than A, this B peak will spread itself out broader than the A peak. For the same reason, the B peak will also be somewhat less tall that the A peak.
![]()
This greater broadening of the B peak (resulting from the faster diffusion rate of the B substance) accomplishes several things. For one thing, it limits the autocatalytic growth of the width of the A peak; this is because the areas immediately around the A peak come to have a higher concentration of B than of A, so that there is therefore a net breakdown of the A substance in these areas (by rule #2, B catalyses the breakdown of A). This results in the formation of a valley around the A peak; we might even call this valley a "moat" since in 2 dimensions it extends completely around the peak; in these locations, the concentration of A becomes lower and lower. Not only does this limit the lateral expansion of any given peak in substance A, it actually leads to the induction of secondary peaks in the concentration of A in the areas just beyond the moat. These diagrams are all taken from an actual computer simulation of this process.
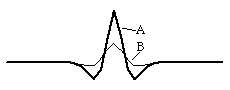
The propagated induction of secondary peaks is probably the most difficult aspect of this mechanism to visualize. It results from the faster diffusion rate of B relative to A, combined with the existence of a "moat" in the concentration of B superimposed on the moat in A concentration. The essential fact is that both A and B diffuse into the moat from the surrounding areas; but since B diffuses faster, this pulls down the B concentration in the surrounding areas slightly more than it does the A concentration. This, in turn, is what initiates the additional peaks; wherever there is more A than B, there will be a net synthesis of both A and B (because of rule #1 above). So a new peak of A (and of B) will form spontaneously on the far side of the "moat". Of course, this new, secondary peak will lead to the formation of another moat on its own far side; the new moat will induce a new peak, and the process will continue.
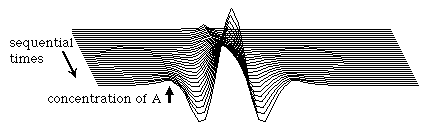
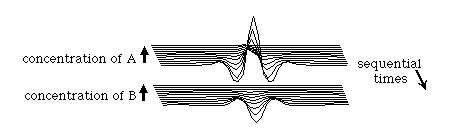
In this example, pattern formation was initiated by a single perturbation at which the concentration of A was raised slightly above that of B. But you could just as well have initiated the process by decreasing A below B, or by either increasing or decreasing B relative to A. Any of these changes will initiate the same sequence of events, although in some cases a valley would form at the site of the original perturbation, instead of a peak. Patterns will also be formed if many different perturbations are made at many different sites, such as if one made random changes in substance concentrations. In that case, the
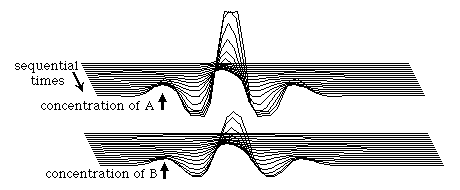
result will also be waves of alternating peaks and valleys of both substance, but the spacing between them will be much less regular than if there had only been a single initiating perturbation so that all the peaks but one had been secondarily induced. Such a time sequence of randomly initiated waves is shown in the diagram below.
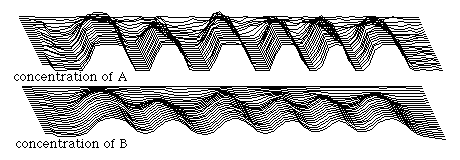
The argument has sometimes been made (for example, see Bard and Lauder, 1976) that mechanisms of this kind would be inherently incapable of producing such regular patterns as one often finds in the anatomical or color patterns of animals. In other words, such mechanisms can produce the irregular blotchy pattern of a Jersey cow, but could they produce anything as regular as zebra's stripes? One counter-argument which can be made to this is that the degree of regularity can be increased by decreasing the number of initiating perturbations, perhaps even reducing this number to only one. Another type of possibility involves changing the rules of the reactions themselves in such a way that they tend to regularize the patterns, so that even when the perturbations are widely and irregularly distributed the eventual pattern which results will have a much greater regularity of spacing than did these perturbations. One approach is to introduce certain non-linearities into the rates by which A and B influence each other's synthesis and breakdown. Another important criticism concerns the demonstrable ability of actual embryos to "regulate", that is to adjust their spacing mechanisms to match the size of the material available to them for subdivision ("size invariance"). Is it possible for such mechanisms as Turing proposed to make the "wavelengths" of their resulting patterns vary in proportion to the total amount of material available?›In fact, we will see that there are actually several ways to accomplish this, although critics may well doubt if any of these are biologically realistic.
Here are some important general principles:
First, what matters are the rules of behavior, not the actual chemical nature of the substances. For example, substance A might be a protein, or an ion, or a nucleotide, or a sugar, or anything else; likewise, B could be any of these. In fact, one can imagine a pattern generating mechanism in which the variables A and B were something other than chemical concentrations: they might be the population densities of two cell types, which stimulated each other's growth and death rates, with one of them crawling faster than the other! Or A could be cell number and B could be physical tension, and so on.›What matters is the rules A and B obey, not their chemical nature.
Secondly, we should not be prematurely concerned with the specific reasons why the molecular concentration might obey these different rules. For example, A might catalyze its own synthesis by activating the expression of a gene, or it might be autocatalytic because it activates an enzyme, or even as a result of having A molecules somehow convert other molecules into additional A. The resulting patterns would be the same.
Thirdly, the set of rules described above is not unique in its morphogenetic powers. Many other, alternative sets of rules of interaction can produce essentially the same effects. The following is another set of rules:
Notice that the location of the peak in A concentration corresponds to a valley in the concentration of B, and›vice versa. (rather than the morphogen waves being in phase with each other, as was the case with the patterns generated by the first set of rules above). In other respects the resulting patterns are almost identical.
Here is still another set of pattern-generating rules:
Only certain combinations of reaction rules have an ability to generate patterns. And not all of these have yet been identified; but there are systematic mathematical methods have been developed by which one can use to look for new ones. Unfortunately, we do still lack experimental criteria for determining whether a given biological pattern was produced by a reaction-diffusion system (or something logically equivalent). This is one of the most serious unsolved problems in the field currently. Another question is whether mechanical instabilities, instead of chemical ones, may produce at least some anatomical patterns directly. The mechanical forces that the cells exert might themselves produce physical instabilities that would produce the anatomical patterns in one step. Increasing numbers of papers have been written on this subject. If you want to know more about any of these questions, please ask.
to the next section, Curvature, contractility, tension and the shaping of surfaces