
One of the most important ways that genes cause anatomical structures to form, and control their geometrical shapes, is by means of mechanical forces. Although we believe that these forces result from genes, some knowledge of engineering concepts is needed to understand why forces create certain shapes, rather than others. These concepts really ought to be included in embryology textbooks; but for some reason, they never are. Knowing these concepts may give you a special advantage in some areas of medicine, including cardiology, opthamology and who-knows-what else.
The key terms are the following: curvature; tension (=tensile stress); stress versus strain; elastic moduli, Hooke's Law, and the distinctions between scalar variables, vector variables, and tensor variables. I will concentrate mostly on mechanical situations in which some kind of internal liquid pressure pushes outward against a flexible surface. There are many examples of this in development, ranging from blood vessels to the eyeball. Somewhat the same equations and concepts may also turn out to apply to structures in which the interiors are not quite liquids, or the surfaces are not so flexible: in this category, I would include embryonic cartilages, most whole embryos, and most individual cells. Once you have learned the key concepts, you will be in a much better position to judge when these concepts and equations do or do not apply.
The key concept here is that the pressure difference across a flexible, stretched surface (like the surface of a balloon) is equal to the curvature times the tension.
Pressure = Curvature * Tension: P = C * T
For example, if we have a balloon, no matter how complicated it is in shape, this equation will be satisfied at every location on its surface. A spherical balloon has the same curvature everywhere; but for any other shape, the tensions and the curvatures will vary inversely from one location to another; where the curvatures are larger, the tensions will be smaller. That means that you could control one variable by controlling the other; so you could make curvature larger in a given area by making tension smaller. And you could make areas of the surface spherical by making the tensions constant. Note that we are assuming that the value of P does not vary appreciably from one location to another; which will automatically be true to the exent that the interior is a gas or liquid, or even a gel (as long as the strength of the gel is small relative to the amount of pressure.
Consider the shape of human eye-balls. They are approximately spherical, but with a bulge at the cornea. Being round allows free rotation in the socket; and the greater curvature of the cornea helps the lens to focus light. Both the cornea and the rest of the eyeball are inflated by liquid pressure, resulting from secretion of liquids and gels inside.

The eyeball and the cornea form separately in the embryo. The eyeballs develop as outpocketings from the walls of the forebrain; and the cornea and lens are formed by areas of somatic ectoderm (that would otherwise have become skin). Midway in development, however, the edges of the cornea become physically linked to the eyeball, as shown in the diagram. Around this time, fibroblasts aggregrate onto the outer surface of the eyeball and lay down layers of collagen fibers, forming a strong layer called the sclera. Other collagen fibers get laid down in the cornea. Experiments have shown that the expansion of the eyeball depends on outward pressure by the liquids and gel secreted into the inside space. Specifically, if a hollow tube is stuck through the sclera into the inside, so that the secreted fluids can leak out, then the eyeball will not enlarge to anything like the normal size. Conversely, I would predict that if you could weaken the layers of collagen, either in parts of the sclera or the cornea, that would cause the eyeball to develop an abnormal shape and/or size, depending on where the weakening was produced.
As part of the mechanism that focuses light on the retina, notice that the cornea bulges out somewhat. In other words, the curvature of the cornea is larger than the curvature of the sclera. If you wanted to make a balloon have this shape, what you would have to do is make the tension smaller in the area that you wanted to bulge out. If you made the tension 20% weaker, then the curvature would become 20% larger. Although it is the balance between pressure and tension that produces and maintains the geometry, to the extent that the pressure does not vary either with location or direction, then the variable that will adjust itself relative to the tension will be the curvature of the surface.
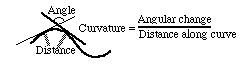
Instead of using degrees as our unit of measure, it turns out to be better to use radians. One radian is 180 degrees divided by the number Pi. The advantage of expressing curvature in radians per distance along the curve is that, when measured in radians per distance, curvature is equal to one divided by the radius of the circle that best fits that part of the curve (which is called the radius of curvature). One over the radius of curvature is equal to the curvature expressed in radians (the distance needed to change direction by one radian). Curvature means angular change in direction per unit length along the line.
The curvature of a straight line is zero. The curvature of a circle is constant. The curvature of a small circle is larger than the curvature of a big circle. The curvature of a parabola varies from place to place along the line.
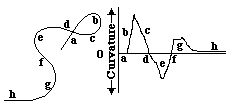
This curve and graph were generated by a simple computer program, written in Pascal, which I will be glad to give you, either compiled (= Mac runnable), or as written in Pascal. I would also appreciate someone's help re-writing these and other programs in Java, so that they can run on IBMs.
The letters a, b, c were put in to clarify the corresponding locations along the curve, relative to the graph of the variations in curvatures along its length. It is arbitrary which parts one regards as having negative versus positive curvature. But it is important to notice how curves bend back on themselves at the location where the curvature changes sign, from positive to negative, or vice versa. Another useful concept is the center of curvature. If you draw a series of lines perpendicular to a smooth curve, these will intersect along another line, called the locus of centers of curvature. Thus the properties of one curve can define a second curve, called its "evolute". Conversely, if curve A is the evolute of curve B, then there is a reciprocal relationship, in which curve B is said to be the involute of curve A. Another noteworthy fact is that if you want to know the approximate radius of curvature of part of a curved line, just trace a series of straight lines perpendicular to nearby points on the line: these will intersect at the centers of curvature of that part of the line, and the radius of curvature equals the distance to where these straight lines intersect.
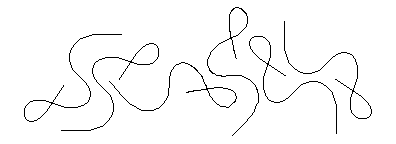
Different lines may have the same distributions of curvatures along their lengths. All six of the curves drawn above have exactly the same distribution of curvatures along their lengths. The beginnings of these curves start at different locations and are oriented in different directions, of course, but otherwise they are all the same curve.
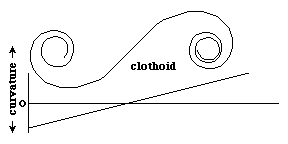
There are many examples of physical phenomena that consistently generate curves of certain shapes. Parabolic paths of baseballs or cannon balls are examples. Among other examples are cases in which curvatures of physical objects vary according to simple equations. The diagram below shows a "clothoid" curve, which can be defined by the property that its curvature increases linearly with distance along the curve. In case you remember the old-style bimetallic strips used in thermostatic controls, their shapes are clothoids; in that case, the reason is that each metal lengthens with increased temperature, and the combination of metals used are chosen so that this amount of lengthening per degree is different. The larger this difference, the larger the rate of change of curvature along the strip; although the shapes will all be clothoids (except of at some unique temperature where the strip will be straight. This shape happens to be the same as those generated by some equations that are important in optics.
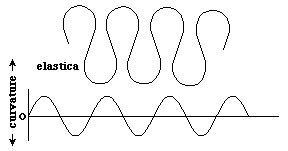
Another such curve, defined in terms of local amounts of curvature, is the elastica. One way to define this is that the curvatures vary as a sign wave; although there are other definitions in terms of the rates of changes of curvatures themselves being minimized, in certain senses. If you start with a long thin metal rod, and squeeze the two ends toward each other, the curves generated are supposed to vary in curvature in this pattern. River meanders are also said to approximate this curve.
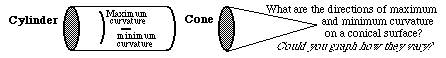
For each location on either the cylinder or the cone, there is one direction in which curvature is zero; in all other directions, there is a (non-zero) curvature, in the sense that the angular directions of tangent lines vary as some function of distance. If you measured all these curvatures, and made a graph of how much larger they were, as a function of the angular direction in which you were orienting your ruler to measure each curvature, you would find that there is a direction in which curvature is a maximum, and this direction is always exactly perpendicular to the direction in which the curvature was a minimum. For these two shapes, the minimum was zero of course. The maximum curvature is constant for every location on the surface of the cylinder. In fact, you could define a cylinder that way: as the shape for which the maximum curvature is constant everywhere, and minimum curvature is zero everywhere. From the embryological point of view, definitions are less interesting than causes: and so please note that if you could cause cells or other materials to arrange thenselves so as to have a zero curvature in one direction, and a constant curvature in the direction perpendicular to this, then this would cause them to form a cylinder.
Notice, by the way, the amounts of curvature in directions that are 180 degrees different from each other will always be equal to each other, inherently. If you think about it for a minute, you can see that this is a logical necessity. On the other hand, it will probably NOT seem like a logical necessity that the maximum and minimum curvatures are always 90 degrees apart. They are however; and it is a logical necessity. Later we will find that directional amounts of tension, and certain other variables, including proportional amounts of stretching and compression, always have their maximum and minimum values exactly perpendicular to each other. Even stranger than that, there are certain equations with which one could predict the amounts of curvature in all the intermediate directions, given the maximum and minimum amounts; and the exact same equations apply to these angular variations of stress, curvature, and some other variables. You don't need to know these equations, however; but it is interesting that they should be exactly the same for what might seem to be completely different kinds of quantitative variables. As we will learn, curvature and stress ("tension") are second order symmetrical tensor variables; all variables that belong to this category vary with direction according to the same set of rules, of which the only one we will learn is that they have their maxima and minimal in exactly perpendicular variables. There are other kinds of tensor variables, they obey somewhat different rules of variation with direction. The higher the order, the more independent the variation with direction.
Please do not memorize the equation shown below, but this is the equation for calculating intermediate directional values of second order tensor variables. A pair of examples are also shown, in which the amounts of the variable in each intermediate direction are shown as a radial graph.
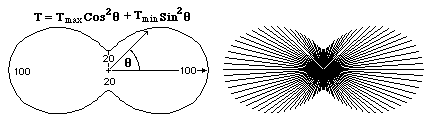
Notice that when the minimum value is less than zero, then there will be 4 intermediate directions in which the amount of tension (or curvature, or whatever the variable is) will be exactly zero in those four directions.
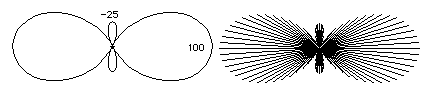
For a cone, curvatures vary with position as well as varying with direction. Each part of the surface has its minimum curvature equal to zero, but the maximum curvature gets larger and larger as we move toward the narrow end. If you could somehow control the amounts of tension in a material, so that the curvatures would vary in the pattern that they vary in cones, then the result would be that the material would remodel itself into one or more cones. From the point of view of developmental biology, that is the point of being interested in curvatures and tensors, etc. how to create geometric shapes by controlling amounts of contractility, or other forms of tension. In other words, if tension and curvature obey a simple equation relative to pressure, then you can generate whatever curvatures you want by making tensions vary according to fairly simple rules. If the pressures can vary, then the equations become a little more complicated; but this increased complexity also allows you to create wider ranges of geometric shapes, by controlling tensions and pressures, and letting the curvatures develop as consequences.
Many people like to say "Oh, it's the genes that tell the cells what shapes to form". The point I am trying to make is that genes may act by adjusting mechanical forces, so that one cannot understand the mechanism without mapping the forces and deducing the rules that those forces obey. Please notice, also, that this situation is different from a person writing by using physical forces to control the where that persons fingers move. Instead of controlling the forces acting at each X, Y and Z coordinate, shapes can be produced by making the cells obey general rules or equations of some kind, with the rules resulting in the shapes. For example, the genes can create sperical structures by having an equal outward pressure, and making the tension the same at all parts of the surface. That is quite different from what is meant by "Positional Information", which would be a matter of choosing the X, Y and Z positions of each part so that a sphere results.
Without doubt, the curvature of the cornea could be changed by mutations in certain genes; and other mutations could cause eyeballs to be less spherical than they are. The question is, do genes create these shapes by adjusting the tensions, and giving the sclera one amount of tension and giving the cornea a smaller amount? This is completely different from the common idea as genes as "blueprints" for structures. Spheres are not the only geometries that can be generated by controlling the strengths and directions of surface contractions. If these forces vary from one place to another, and even more so if the forces are stronger in some directions than others, then there are no known limits to what shapes can be generated.

The shape drawn above has approximately the same combinations of directional curvatures as a football. It is also the same shape as lemons and as the masses of spores at the tops of the stalks of Dictyostelium fruiting bodies. Later in the course, we will find out the vertebrate limb buds go through a series of shapes related to these. As an exercise in thinking about curvatures, and how curvature can vary from place to place, and also vary with direction, try to sketch the graphs on the right, below: for each point along the gray horizontal line. Can you figure out what are the maximum and minimum curvatures at each location?

A more difficult question to ask yourself is whether there are certain rules by which tensions could vary, with location and/or direction, that would cause materials to arrange or remodel themselves into shapes that have this distribution of surface curvatures.
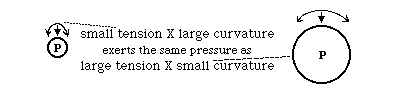
In blood vessels, the outward pressure of the blood is held back by the combination of tension and curvature of the wall of the blood vessel. This explains the paradox that the walls of capillaries are so thin, even though the pressure they resist is almost as large as in arteries. The walls of arteries have many layers of smooth muscle cells, fibroblasts and tightly-wrapped collagen fibers, in addition to the thin endothelium directly adjacent to the blood itself. In contrast, capillaries only have this thin, weak endothelium. The key concept is that the diameter of the capillary may only be a hundredth or a thousandth the diameter of the artery, and therefore the curvature of the wall of the capillary is a hundred or a thousand times larger. That means that a given amount of outward pressure will only produce a hundredth or a thousandth as much tension in the wall.
In this equation, C and c refer to the amounts of curvature in the directions in which curvature has its minimum and maximum values. So C is the amount of curvature in a certain direction, and T is the amount of tension in that same direction; and c and t refer to the amounts of curvature and tension in the directions perpendicular to the first directions. Notice, however, that this equation assumes that the direction of maximum curvature is the same as either the direction of maximum tension, or at least as the direction of minimum tension. But these directions are not obliged by any laws of physics nor of mathematics to be the same for tension as for curvature. Having learned that the maxima and minima of each variable always occur in perpendicular directions, one might not be too surprised at this point to learn that some analogous restraints force tensions to have the same maximal directions as curvatures, or something like that. There is no such restriction, however, even though that equation is widely used, and is not quite correct unless the directions of maximum curvature are either the same or perpendicular to the direction ot maximum tension.
In cylinders, among some other shapes, these maxima do happen to have the same directions.

As discussed above, curvature of a cylindrical surface is zero in the longitudinal direction, and a maximum in the circumferential direction. The amounts of tension produced by outward pressure on the walls of a tube turn out to have their maxima in the circumferential direction and their minima in the longitudinal direction. In neither direction are the tensions zero. however. Instead their ratios tend to be close to 2 to 1, in other words, twice as strong in the circumferential as in the longitudinal direction. In an actual pipe, the amounts of stress in the wall need not be in that exact ratio; but that will be the ratio of the amounts of stress produced by the outward pressure. In other words, when you push water down a pipe, the amounts by which you change whatever tensions previously existed in the wall of the pipe will be exactly two to one.
Notice that when we apply our equation ( P = C*T + c*t) to this situation, one of the curvatures is zero, so the amount of tension in that axis does not contribute to resisting the outward pressure. In other words, c is zero, so P = C*T
Likewise, if you had a situation in which t were zero, then only C and T would contribute to the pressure difference. In the more general situation, both curvatures and tensions have non-zero values.

The to answering this question is to realize that the cleavage is caused by circumferential contraction (like a belt tightening around the cell's equator). Now that you realize that both tension and curvature vary with direction, and know that inward force is equal to tension times curvature, you should be able to see that whatever amount of tension is being exerted across the furrow (in the longitudinal axis) is tending to resist the constriction of the equator. In other words, the net inward force around the equator is equal to the circumferential tension multiplied by circumferential curvature MINUS longitudinal tension multiplied by longitudinal curvature. Of course, the circumferential tension must be stronger than the longitudinal tension; but how much stronger? The two perpendicular curvatures tell us the answer; since these curvatures have a ratio of one to ten, and the difference between them is such as to hinder further constriction of the equator, yet the constriction does continue, therefore the ratio of the directional amounts of tension must be AT LEAST 10 to one, so as to overcome the opposite ratios between the perpendicular curvatures. Most people who study cell division, in my experience, do not understand how to think about directional variables; they think of tensions as having certain amounts at each location.

Having only one value of T makes our equation for pressure simpler. Since tension is the same in every direction and location, only the curvatures can change. Within any one bubble, even when it is distorted by external objects, as shown in the diagram above, both T and P are the same everywhere. That means that C + c = P/T = some constant. In a spherical bubble C = c, of course. But for more complicated shapes, C and c both change from one location to another; but both curvatures adjust themselves so that the sum of C and c are constant. When one gets big, the other gets small, etc. And when one gets bigger than P/T, then the other becomes negative. The system behaves as if the material were constantly recalculating the equation C + c = a constant, and changing both curvatures so that their sum will always be a constant.
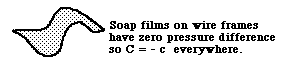
If the pressure difference between the two sides is zero, then C + c = zero. Another way of saying the same thing is that C = minus c.
The shapes formed have the minimum total area for any shape that has that margin. A Belgian mathematician of the later 1800s focused his attention on this question, and it is named after him: "Plateau's Problem". One way of stating the problem is to ask what shape a surface would need to be to have the minimum total area for an arbitrary defined edge, in the sense that if somebody specified an equation for the positions of the edge, the problem would be to calculate from that an equation for the surface that intersects that edge and has the minimum possible total area. This problem occupied the attentions of many great mathematicians, and several books have been written with the name "Plateau's Problem".
It seems odd that soap films should be able to calculate this shape almost instantly, when mathematicians have so much trouble calculating it. There are fairly easy ways to calculate the shapes by successive approximation, however. All you need to do is simulate the behavior of a sheet of material, each part of which exerts pulling forces on its neighboring parts. If your computer program constantly recalculates the X, Y and Z coordinates of each part of the sheet, while leaving the margins in some arbitrary positions, then the computed "pulling forces" will produce the same shape as a soap film would. The results of several such simulations are shown below, with a variety of arbitrary geometries imposed on the edges, including combinations of sine waves and straight lines.
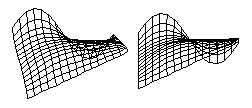
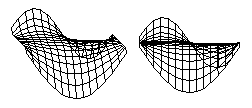
Some cells and organisms have shapes with constant mean curvatures, as first noted by D'Arcy Thompson. This implies that their shapes result from some kind of contractile tensions in their surfaces, and moreover that the strengths of these tensions are more or less isotropic and homogeneous. It does NOT imply anything about the physical cause of these surface forces however. Unfortunately, that is what has usually been concluded. Thompson never says exactly what he thinks it means; but he was notoriously impatient with evolutionary explanations for shapes; and he certainly allows his readers to interpret shapes as the direct result of surface tensions, in the literal sense of being the same force that contracts the surfaces of soap films.
Therefore I want to stress two things:
First, that the shapes produced do not depend on what specific force contracts the surfaces. The shapes of soap bubbles and liquid drops result from the contractility of their surfaces having the same strengths in all directions and at each location. Any force that does not vary with direction or location would produce exactly the same shapes. Such a force could perfectly well be produced by layer of actin and myosin, or by stretching of some elastic or plastic material. Therefore, when cells have these shapes, that is not evidence that surface tension (in the literal sense) has anything do do with causing their geometry. Any isotropic force will produce the same shapes. Historically, however, most people have interpreted such shapes as meaning that they must be caused by the same specific forces as in bubbles.
Second, a much wider range of additional shapes could be generated by forces that are able to vary with direction, and/or to vary from place to place. In the case of the eyeball, we saw that you can get a spherical shape by making tension the same everywhere (in an inflated object), and you can make one part bulge out by making the tensions smaller in that part. Cylinders, in constrast, have directional variations in the tension of their surfaces. Thus, just as cells will tend to form spheres if the tensions in their surfaces are constant with position and direction, cylinders ought to result if the tensions at the surface tend to become twice as strong in one direction as in the perpendicular directions.
Historically, D'Arcy Thompson's approach has been a dead end because he either did not notice or did not mention these two key points: that the shapes he observed imply only what rules the forces obeyed, not what generated the forces; and that (many) other anatomical shapes could equally well be generated by intrinsic forces, IF the forces obeyed more complex rules. Unfortunately, the possibility of generating shapes by internal forces only occurred to him for those few shapes that are recognizably similar to soap bubbles.

Does this mean that groups of cells whose surfaces contract twice as strongly in one direction as in the perpendicular direction will therefore "automatically" arrange themselves into cylinders?

Hint, can both perpendicular curvatures ever be negative. What is the anatomical basis of dimples?
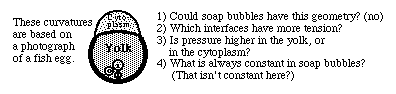
If you make a graph of stress as a function of strain, it tends to be a straight line, as long as the amount of distortion is small (like 1 or 2%). This linear proportionality is called "Hooke's Law", after the scientist Robert Hooke who lived at the same time as Newton. The slope of this straight line is called the elastic modulus, or "Young's Modulus" for the particular case of simple stretching or compression. Thus rubber has a low Young's modulus and steel has a large one. There are other moduli for shearing forces and volume changes. In fact, even though this variable is often treated as if it were simply a scalar variable, really it is a fourth order tensor. Even to the extent that Hooke's law is precisely obeyed, and even in pure materials, the slope of this curve as apt to vary with direction by many tens of percent. The directional variation obeys equations that are more elaborate than for second order tensors, and have trigonometric sines raised to the fourth power, instead of just squared! So be glad we won't tell you about them.
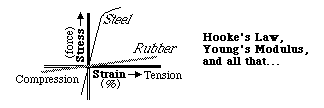
Don't think of this linear proportionality as a law of nature; it is more of a rule of thumb, an idealization and a simplifying assumption. It is more like the ideal gas law than the law of gravity. If you don't stretch or squeeze materials too much, so that strains are less than one or two percent, then the strengths of their internal forces that pull or push (or twist) them back toward their rest lengths (and shapes) can be quite close to linearly proportional to the amount of strain. Materials that obey Hooke's law are said to be "Hookean"; and materials that depart from this rule are called "non-hookean". Any material becomes non-hookean when the strains are large enough. Many materials are non-hookean beginning with even the smallest strains. The limits on hookean behavior tend to be only one or two percent. Biological materials are notoriously non-hookean, besides which very large strains (tens of percent, or more) often occur in biological phenomena.
Please do not think of non-Hookean behavior as in any sense contrary to the laws of nature; a better analogy would be the ideal gas law, which is accurate at low pressures and high temperatures, but becomes wildly inaccurate at higher pressures and lower temperatures, as when liquids form. After all, according to the ideal gas law, liquids shouldn't exist. Obviously, you can't predict weather based only on the ideal gas law (among other things, rain would be an impossibility!). Likewise, we should expect that many important biological and embryological phenomena will depend precisely upon disobeying Hooke's law. Non-linearities are powerful sources of interesting behaviors of materials.
Musical instruments depend on this linearity . Whatever parts of them vibrate have some kind of mechanical stress driving them back and forth; and linear proportionality is necessary in order for the resonant frequency of each part's vibration to remain the same independent of loudness of the noise. The louder the sound produced, the farther the distance that the vibrating parts are moving back and forth; and therefore the faster they have to move in order to cover the greater distance in the same fraction of a second. If they go twice as far, then unless they go twice as fast, then the frequency of the sound produced will be different. Linear proportionality between strain (the distance they have to vibrate) and stress (the forces that cause the speed) will keep frequency the same, despite the different distance. Conversely, non-linearities in the graph of strain versus stress (non-hookean elasticity) will shift the resonant frequency as the instrument is played louder. If you think about it carefully, you should be able to see how to deduce the direction of this non-linearity (whether twice the stress results in more, or less, than twice the strain) based on whether the resonant frequency goes down or up slightly when you play the instrument louder.
Unfortunately, nearly all such complex engineering equations are based on three specific simplifying assumptions. One assumption is that all strains are less than about 1% This is usually not true in biological situations, and never can be true in embryology, to the extent that it concerns enlargements of structures by hundreds of percent. Another assumption is Hooke's law: linear proportionalities between stress and strain. Not only is this false for all materials at more than a few % strain, but larger-scale qualitative behaviors of materials often result precisely from these non-linearities. Convexities in these curves can have bigger effects than could result from many-fold differences in the slopes themselves. The third false assumption is that properties of materials don't vary with direction. Even for wood, elastic moduli and strengths can easily vary as much as 5 fold from one direction to another. In fact, even pure metals can vary 20 or 30% with direction.
If all these equations are so unreliable, then why don't more buildings fall down. Part of the answer is that engineers deliberately chose materials to obey simple equations, not just for strength. Warping is an example of materials developing "a mind of their own", and is never considered desireable. Another part of the answer is that engineers make things 5 times as strong as their equations tell them would just barely be sufficient. (for airplanes, this standard ratio is only 3) Therefore, if the equations are wrong by 50% or even 100%, the buildings still don't collapse.
If engineers had to predict exactly at what load their structures would collapse, their current equations wouldn't be accurate within 50 or 100%. That doesn't mean that biologists can't use those equations for some purposes, such as to perceive qualitative advantages of certain structural arrangements. Embryology, among all sub-fields of biology, should trust these equations least than any other field. To the extent that anatomical shapes are created by yielding to internal forces, they lie exactly in what we might call "the blind spot" of engineering.
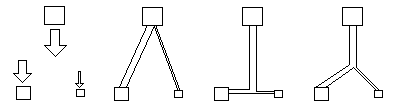
From the point of view of using the least amount of metal for a given amount of flow, or rather the least resistance to flow for a given amount of metal, some kind of Y-branch would be better than either the V or the T patterns. In fact, one could calculate the best angle of the Y bend, as some function of the relative amounts of liquid that one wants to have flow to the two goals. Of course, in the real arterial system, there are many more than just two locations toward which arteries carry the blood. That makes the optimization problem that much more complex. But mathematicians have developed systems for finding such optima, given just about any goals or constraints. This general subject is called "The Calculus of Variations", and there are whole textbooks about it (and even journals!). In the case of arteries, it is claimed and widely accepted that their actual branching and relative diameters really do optimize the use of material. The resulting angles of branching are called "Murray's Law", after the British biologist Cecil D. Murray (J. Gen Physiol. IX pp 835-41, 1926). I have read this and another paper by him, and I have my doubts about the accuracy of his measurements.
Nevertheless, the diameters and angles of branching do show consistent patterns, of the Y-branch pattern. And these give me a strong aesthetic impression that some consistent equations are being obeyed. Therefore let us consider several different kinds of underlying mechanisms.
One type of optimization would be strictly Darwinian. By this, I would mean that the specific positions of each branch point and each diameter would be specified by the genes, on a point to point basis, in the same sense as a blueprint would specify positions, angles, diameter, etc. If that is the sense in which genes specify anatomy, then optimization would be achieved by trying large numbers of different actual geometric arrangements. That would be equivalent to building actual pipelines in all the different patterns, pumping liquids through each of them, finding out experimentally which pattern results in the most flow for the least amount of material used, and then adopting this best pattern for all future use.
A different and more interesting cause of optimization would be if the contractility of the arteries themselves tended to produce the best possible combinations of branching angles. This could be easily accomplished by having the longitudinal tension in each artery vary as the correct function of diameter. That would make the optimal branching angles arise automatically. It would be the equivalent of an analog computer solution to the problem. Please try to invent some possible experiments to test whether this is the kind of mechanisms that controls the embryonic development of these angles. Ask yourself whether the eventual amount of tension along the arteries will be any different, depending on whether the angles are created by some completely different mechanism, or by means of adjusting the tensions so as to get the right angles.
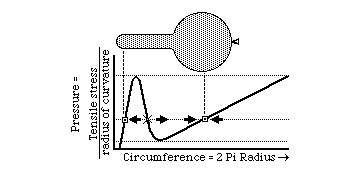
Aneurisms are closely analogous to what happens when you partially inflate an elongate balloon. Almost everyone is familiar with this situation. One end of the balloon becomes fat and round, and feels as if the inside pressure were much more than at the thin, limp end. Few people will admit that they don't understand why this occurs. Another good question is why so much more pressure should be needed to start blowing up a balloon, but then it gets easier. Some people will tell you that the pressure really is higher at one end than the other. Another misinterpretation is that it has something to do with stretched rubber becoming weaker, or something like that. Neither has much relation to the truth.
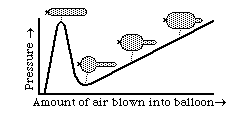
The key to understanding such events is the inverse proportionality between curvature and tension in the surface. The outward pressure is the same everywhere; but in the more swollen part, the curvature is less; therefore more tension is created in balancing this pressure. Tension increases almost linearly with the stretching; so you have two variables that are both increasing linearly; one is radius of curvature and the other is the mechanical resistance to stretching. The qualitative behavior of the system depends on on small non-linarities, where one effect gets a little ahead of the other. In the case of aneurisms, life or death hangs delicately upon slight departures from linearlity.