The following are some engineering and mathematical concepts that embryologist need
(but don't usually know anything about)

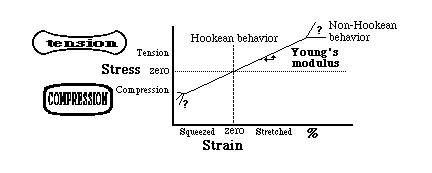
Stress = mechanical force per cross-sectional area.
Either tensile stress or compressive stress can occur.
It has units of force per unit area.
You can define tension as positive and compression as negative
(or you could define them the opposite way, just as well)

Strain = proportional stretching or compression, produced by stress
By what % has a material lengthened or shortened. (or sheared)
If all stresses were relieved, then how much would dimensions change

Young's modulus = the slope of the curve of stress per strain
so rubber has a small Young's modulus, steel has a large E

Hooke's law is linear proportionality of stress to strain
If Young's modulus is constant, then a material is "Hookean"
But real materials are never Hookean beyond 1 or 2% strain.

Curvature = angular change of the tangent line per distance

(angular change per distance along a curve)
the radius of curvature = 1/divided by curvature
(and has units of distance per radian of angular change)
A straight line has zero curvature. A circle has constant curvature.
Curvature of small circles is larger than curvature of a big circles.
Curves can be defined by the amount of curvature at each point.
(Negative curvature means the line has curved back on itself)
A cylinder has zero curvature in the lengthwise direction;
and has constant curvature in the circumferential direction.

In other words, the local amounts of stress automatically adjust according to the local amounts of curvature, so that one multiplied times the other is a constant everywhere.
To the extend that the material is flexible, & pressure is constant.
If tension (=stress) becomes larger, then curvature becomes smaller.

-----------------------------------------------------------------------

A brief review of concepts and vocabulary:

Stretching something produces (increases) both what and what?                    both start with S

Bending something increases what variable?                                 that starts with a C

If pulling twice as hard on something always increases its length by twice as much,
then the material is said to obey whose law?                                      starts with H

Do all materials really obey this law?                                                   Not by a long shot.

Is the graph of stress per amount of strain always a straight line?                           nope

If this graph is a straight line, then the slope is called what name?                           E

* Can the amount of stress in a material vary with direction?                                sure

* Can stress in a material be negative as well as positive?                         you can define it that way

For a parabola or an ellipse, or other geometric curve,
could you make a graph of curvature as a function of distance?

* If you started with a graph of curvature as a function of location,
could you sketch what a curve would have to look like?

Can the curvature of a surface be different in different directions?                           yes

* On spheres and flat surfaces, does curvature vary with direction?                   no, but only for them.

* What about the surface of a cone? How large is the curvature in each direction? The circumferential direction? Longitudinal?

** If you stretch a soap film across a bent wire loop,
then the pressure is the same on both sides of the curved soap film.                                                              (yup, it is)

** If the pressure difference from one side to the other is zero,
then shouldn't the curvature also be zero?                                         (No! But why?)

Pressure difference = Stress * Curvature ?
so if pressure difference = zero
then does stress * curvature = zero

But a rubber film DOES have curvatures, & also has constant stress

Don't be frightened by the following advanced mathematics;
you only need to understand the basic ideas.

Scalar properties include temperature & chemical concentrations
At each point in space, the temperature is some amount
But this property doesn't vary with direction, nor have a direction.

Vector properties have an amountand a direction at each location.
Like wind speed is 12 mph toward the northwest.
Electric and magnetic fields are also examples of vector properties.

Tensor properties have an amount in each direction.
Such a property might be 12 units in the direction North-South
And be minus five units in the direction East-West

Or it might be 12 units in every direction, or zero in some directions

But what are some examples of properties that are tensors?

And are there even more complicated properties, beyond tensors?

And are there any limitations on how tensors vary with direction?

Suspense!!!!!

What are some examples of properties that are tensors?

Stress, strain, curvature and Young's modulus are tensors.

And are there even more complicated properties, beyond tensors?

Stress , strain and curvature are "second order tensors".

Young's moduli are "fourth order tensors".

Scalars are zero order tensors
Vectors are first order tensors
(certain vectors are really second order asymmetrical tensors)
In other words, what's beyond tensors are higher order tensors.
For example, ratios between second order tensors are fourth order.

A ratio between a third order and a second order tensor would be a fifth order tensor. A ratio between 2 fourth order tensors would be 8th order, etc.

Are there any limitations on how tensors vary with direction?

The higher the order of tensor, the greater the degree of independent variation is possible as function of direction.

Second order symmetrical tensor variables vary with direction in the same pattern as second derivatives

Third order tensors vary in the pattern of third derivatives.

Vectors vary in the pattern of first derivatives.

Some related concepts are the potential of a vector field, the curl of a vector field", the fact that vectors have potentials if and only if their curl is zero at all locations, the divergence of a vector field, the gradient of a scalar field, the fact that if "A" is the gradient of scalar field "B", then B is a potential of A, and A has zero curl. The divergence of a gradient ("div grad") is the Laplacian, which is equal to the sum of the second derivatives in all 3 dimensions, & diffusion of a variable causes values of its Laplacian to approach 0. Maxwell's equations use div and curl to explain electromagnetism Eventually, developmental biology will have to catch up with this.
( But is isn't even headed that way, at the moment)

Tensors get their name from tension having been the first tensor property to which the concept was applied. Calculus, vectors, etc. were all developed as methods for analysing situations in astronomy, physics and engineering. There is a good book named "Div, Grad, Curl, And All That" Embryological questions sometimes can be solved with these older mathematical concepts; but sometimes they are over-simplifications & new mathematical concepts will need to be invented.

Most mathematicians know zilch about the history of their own field and tend to want to bully people, instead of help them understand. Unfortunately, most "Applied Mathematicians" insist of clinging to existing mathematics, instead of help designing experiments. They assume problems are questions of "true or false", even the real questions are "oversimplified or not" or "applicable or not".

Why is a soap bubble spherical?

Its shape results from a counterbalance between 2 opposed forces.

Air pressure on the inside, pushing out equally in all directions.

Tension of the soapy water surface, pulling equally in all directions.

Why are balloons sometimes NOT spherical, but other shapes?

When the stress in the rubber exerts equal force in all directions
and at all locations then the balloon will be spherical.

In other words, if the forces have a certain symmetry,
then they will produce shapes with this same symmetry.

If stress is stronger in some parts of the rubber
OR if the rubber's stress is stronger in some directions that others,
either or both of these can cause non-spherical shapes to exist.

Asymmetry is at least one of the forces is needed to produce asymmetry of the balloon (the same would be true of embryos)

Forces have symmetries, but not actual shapes.

In a cylindrical balloon, stress is exactly twice as much in the circumferential direction than in the longitudinal direction.

The air pressure inside is not capable of exerting a stronger force in some directions than in other directions. It has spherical symmetry.

The key point: Bubbles are spherical because the forces that cause them have spherical symmetry.

In order to blow square bubbles, or even cylindrical ones, you would either have to make the inside pressure differ with direction, or you would need to make the stress in the soap film be different in different directions. Soap and rubber molecules do not contain blueprints for spheres.

Symmetry concepts: There are many different kinds of symmetry

The exterior of our anatomy has one plane of reflection symmetry.

Most starfish have five planes of reflection symmetry.

Some jellyfish have 8 planes of reflection symmetry.

The capital letters N, S and Z have two-fold rotational symmetry.

A ladder has displacement symmetry. So does a centipede.

A zig-zag has "glide-reflection symmetry"

A snail shell has a combination of rotational and dilation symmetry.

Each kind of symmetry is defined in terms of a symmetry operation.

Reflection is a symmetry operation; rotation is another symmetry operation; magnification (=dilation) can be a symmetry operation; displacement by a certain amount in a certain direction is the operation in terms of which displacement symmetry is defined

The point is whether the object "looks the same" (and is geometrically superimposable to what it had looked like before) after you apply a given operation.

If you want to invent new kinds of symmetry, then you have to invent symmetry operations (like maybe shape changes produced by some distorting mirror or lens, could be a new kind of symmetry)

Symmetry has very profound implications in advanced physics.

For example, the law of conservation of energy results from forces of nature having certain symmetry properties. If gravity pulled asymmetrically, energy wouldn't be conserved. Conservation of momentum, angular momentum, charge, and two other variables (having to do with sub-atomic particles) are all conserved. This is more profound than thinking about 6 different magic fluids being conserved. Read Weyl, Feynman or Joe Rosen to know more.

THIS IS NOT A PHYSICS COURSE, HOWEVER so don't worry about conservation laws.

Madame Curie's husband was Pierre Curie, and he invented Curie's Principle

"Effects have the same symmetry as their causes"
(or sometimes even a little more symmetry, but NOT less)

However, embryos have special methods to break this law.

The difficulty is not how to make objects become less symmetrical!

Bubbles and balloons get much less symmetrical when they pop

Breaking an axially-symmetrical glass tube produces fragments that have no symmetry left at all!

How to get around Curie's Principle, without becoming random.

The problem is how to break symmetry (become less symmetrical than either the object or the combination of forces acting) but only break it a little bit, so that you consistently end up with the same shapes each time.

Embryos of many species start out as spheres.
(which does not mean that they are made of soap or rubber, or that they have "surface tension", or that they are temporarily transcribing genes for roundness, or round blueprints!)

Many major events in development break symmetry;
the developing embryo loses some symmetries and keeps others.

Gray crescent formation (and then gastrulation) is a replacement of axial symmetry with bilateral symmetry. (the embryo used to have an infinite number of planes of reflection symmetry, but now it keeps only one plane of reflection symmetry.

Kelp eggs (brown algae) start out with spherical symmetry, and use external signals to reduce this to axial symmetry.

Somite formation breaks displacement symmetry, changing paraxial mesoderm so that it has only some certain wavelength.

Flagellar basal bodies are used to break reflection symmetry, so that the aorta leaves the heart from the left side, etc. Kartegener's syndrome and all that.

Any time a developing embryo becomes LESS symmetrical than it had been, we should try to figure out the mechanism, and what such mechanisms have in common with each other.

The following is one category of mechanisms for reducing symmetry, especially for reducing displacement symmetry

Reaction-Diffusion systems:
Invented by Alan Turing, copied by Hans Meinhardt & others.

Imagine the following situation:

There are two diffusible chemicals, "substance A" & "substance B".

At first, the concentrations of both of them are the same everywhere

At each point in space, their concentrations change according to the following three rules:

1) A stimulates increase in amount of both A and B

2) B stimulates removal, breakdown, loss, etc. of both A and of B

3) B diffuses faster than A diffuses.

What will happen? Will anything happen?

More suspense......

The result will be formation of waves of higher and lower concentrations of both A and B.

A and B don't have to be concentrations of diffusing chemicals.
They could be numbers of two different cell types, one of which crawls faster than the other.
A could be stress and B could be curvature, and one could act at longer range than the other.

Reaction-diffusion mechanisms can also break symmetry in spherical embryos, if wave-length is large relative to total size.

Some general conclusions, for reviewing today's lecture.

1) Embryos use mechanical forces to create anatomical shapes.

2) We need to borrow engineering concepts to understand this.

3) Stress and curvature are two of the most important concepts.

4) Some properties can vary with direction (tensors can, but scalars can't).

5) Many different kinds of symmetry are useful in physics.

6) Forces and other causes often have certain symmetries.

7) Curie's principle predicts that shapes will be as symmetrical as whatever forces cause them to exist.

8) Becoming randomly less symmetrical isn't difficult.

9) The difficulty is how to become less symmetrical, and have the results come out the same very time.

10) "Reaction-Diffusion systems" are an example of selectively amplifying random variations, to generate regular patterns. (breaking displacement symmetry)

11) "Blueprints" are the wrong analogy for understanding how genes cause the formation of the body.

12) Textbooks don't have much of a clue about this kind of stuff.
("somites are caused by the noggin protein")
("right-left asymmetry is caused by flagellar beating, and the lefty protein" etc.)

Right, and hurricanes are caused by air. As Pauli once said: "It's not even wrong."

Note:

Our textbook does cover Turing's reaction-diffusion mechanisms, but doesn't seem to understand that they can generate regular patterns even starting from homogeneous concentrations, and certainly not that they work even better with tensor variables as compared with chemical concentrations.

In general, Biologists have been so astonished that such a simple combination of chemical reactions (A causes synthesis of B, etc.) can generate spatial patterns, that they tend to assume that only this one combination of equations can do it. Look at the drawings on page 21, which are not even actual computer-generated patterns, and are very misleading. He even calls the chemicals "S" and "P", as if to imply that only certain sorts of chemicals can have the effect. Actually, the two variables don't even have to be able to diffuse; it is sufficient for them to produce stimulatory and inhibitory effects at different ranges.

Computer simulations of these and related versions of reaction-diffusion systems are available from me for Macintosh computers. And if anybody knows enough about programming to re-write some of these to run on PCs, than we could post them on this web site.